Information Theory refers to some bullshit from the early 1900s by Claude Shannon et al. He basically formulated communication as such:
From this we learn, among other things, how to analyze communication statistically, thanks to the statistically defined noise addition function. This was further used to show (skipping a lot of details) that information is most efficiently transmitted in binary. As applicable as this model may be, the lessons it has to give have already been absorbed into the culture at large, and so I won't waste your time with them.
Instead, I wish to answer perhaps a more provocative question: What is the structure of the unencoded information? What is going on inside Alice's head when she consideres an idea, in the abstract sense?
We know, at least, that such an idea has to at least have some sort of structure, as there is some function (Alice's Encoder) which maps it into a space that is actually mathematically well-defined. The pre-image of that space under the encoder must also be some sort of formally definable superspace, which itself is a subspace of the whole space of the possible idea. That's a lot of words to hand-wavily say that there has to be some formal structure to the space of ideas that Alice can have. Then, in practice, what is an element in a space of ideas?
I now define modality and register. Modality refers to a format of information before it has been encoded for transmission. A register is a more specific type of modality, with emphasis on the style of encoding used.
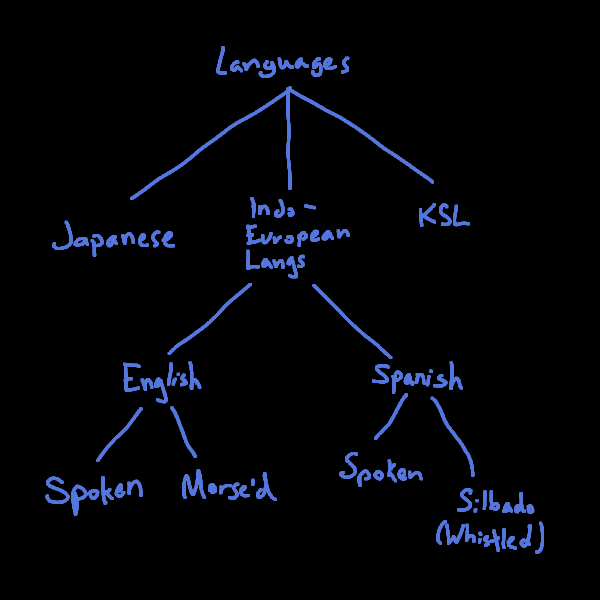
Some common examples of modalities:The English Language. A language is a structured set of permissible utterances up to its grammar. It is worth noting that language in abstract is not a modality. Just because one understands the space which grammatical english sentences occupy does not imply whatsoever that he understands that of some other language. There are some genuinely untranslateable structures (e.g. 教師の教, to specify a kanji, in spoken Japanese.) Furthermore, there is no good homeomorphism, so-to speak, between grammatical productions of any pair of unrelated languages. We will develop some more theory later to hopefully make this claim more intuitive.
Within the modality of English, there are many registers. There is the written register, with sub-registers of script and cursive (which can be yet further subdivided,) the spoken register, the register of morse code, binary code, and plenty more. Other languages have different common sets of registers, for example on the Canary Islands, there is a whistled register of Spanish.
Board Games. Not as many people know these at a sufficiently deep level, but I can hopefully shed some light with some quotes about Go, which demonstrate that games actually can be interpreted in a deeper way than any layman may perceive them.
The board is a mirror of the mind of the players as the moments pass. When a master studies the record of a game he can tell at what point greed overtook the pupil, when he became tired, when he fell into stupidity, and when the maid came by with tea.
Nick Sibicky, paraphrased, regarding AlphaGo:
I had a moment, right? I was reading a bunch of these games back to back. And where I truly felt like... Woah. We are communicating with something else. Like, something alien. And Japanese have hand talk, right, go as an act of communication? And I just had to stop, like, I'm done. This is weirding me out. 'Cause we are talking with something. Through these games. So I had an alien encounter kind of moment when realizing that this thing speaks a different language.
Music. With this example, we depart further from traditionally communicative modalities. That said, it is still clearly a format of information.
You are very capable of recalling data (up to your choice in register) in modalities which you have acquired. Modalities permit for the patterning of information mentally, and so they result in a high ability to recall. This is the reason that chess players (and less commonly, go players) can play blindfolded games. It is not because they have memories infinitely better than the rest of us, but instead because the patterns on the board are as inherently meaningful to them as a sentence in our native language or a catchy tune. Similarly, if you take a good rubik's cube solver, tell them to inspect the cube in preparation for solving it (a common practice,) and suddenly blindfold them without their knowing, they can likely tell you exactly where a lot more pieces are than you could, even if you were explicitly trying to memorize for such a feat. That state on the cube is more than noise to a skilled cuber: they interpret the cube as meaningful and actionable information at the level of perception.
It is quite difficult to actually formalize the amount by which this aids memory. An English sentence, spoken, contains an enormous amount of information at many levels of resolution: vocal timbre, intonation, actual semantic content and so on. I have no doubt that the amount of information memorably transmitted exceeds the average ~25-bit human memory bandwidth for numerical recall with enormous margin.
Modalities tend to feature some idea of grammaticality. That is to say, they have distinguish between elements which are, and are not, grammatically permissible. Cacophonous random noise is not permissible under the grammar of music, "Strength I of sam pig" is not permissible in English, and a go board with stones scattered randomly would not be grammatical under the modality acquired by a professional. This will be a theme to watch out for going forward as we eventually examine some modalities which do not feature a grammar.
All of them are acquired. That is to say, we are not born with them, but rather through mass input, gain the ability to discriminate between grammatical and ungrammatical elements. This is not so strictly true of music, but it seems at least partially the case: note cross-cultural differences in tonal interval, and music more generally. Permissibility isn't strictly the same between cultures.
Now, a question worth asking is: what can modalities look like? Could we taxonomize them? Now that you have hopefully gotten a gist for what they feel like, here is a long list of modalities, rapid-fire:
Now that's great and all, but they won't teach us much in a list. Let's try to organize them. English and English Morse are obviously very similar as they are registers of the same underlying modality. The same can be said of Spanish and Silbo Gomero. Japanese is quite similar and Kenyan Sign Language a bit further off. We can translate between them, and at least for Spanish and English, we can do it with very high fidelity thanks to shared history. We thus have:

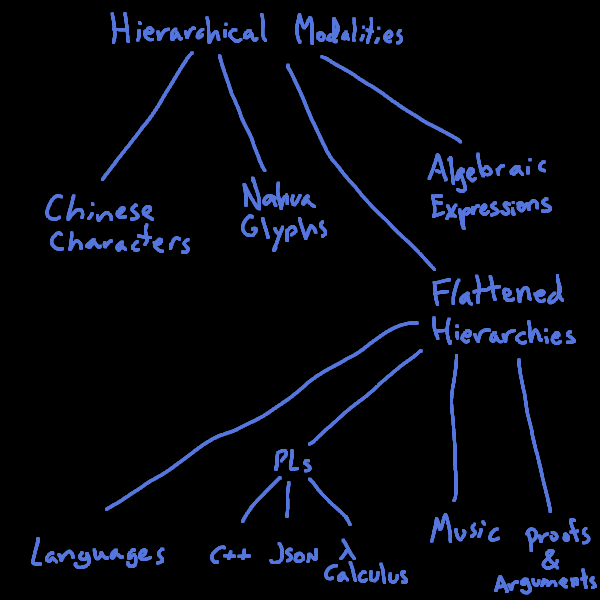
Insofar as spoken language is a way of compressing a grammatical parse tree into a linearly-organized sequence of sounds through time, some other "flattened trees" may be the nearest modality-cousins of languages: Programming Languages, Music, Lambda Expressions, and Mathematical Proofs. JSON could be considered in this category too, but it doesn't have such strict and complex grammars as the others in the category.
Slightly more distantly related must be Chinese Characters, insofar as they have a hierarchical structure (although not flattened into a string) along with a clear sense of grammaticality. The same can be said of Nahua Codex Glyphs and Mathematical Formulas.
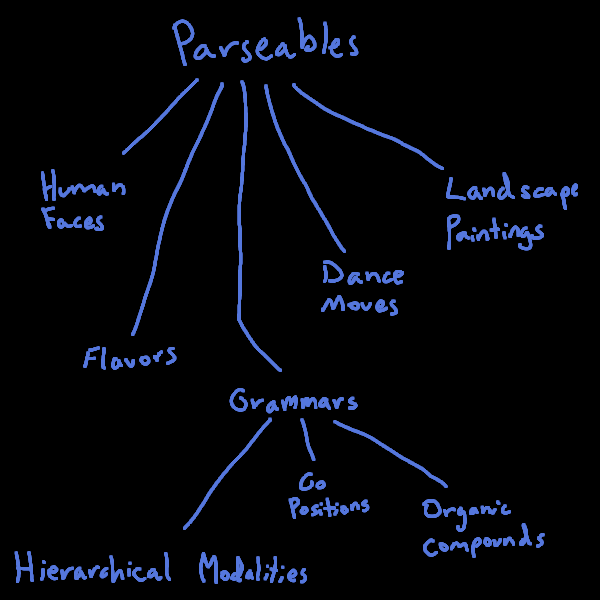
More distant yet are Organic Compounds and Go Positions, which both feature grammaticality but are not of an obvious hierarchical form. These, along with all of the above, are elements of what I call the "parseable structures," but so are some non-discretized objects like Human Faces, Landscape Paintings, Flavors, and Dance Moves.
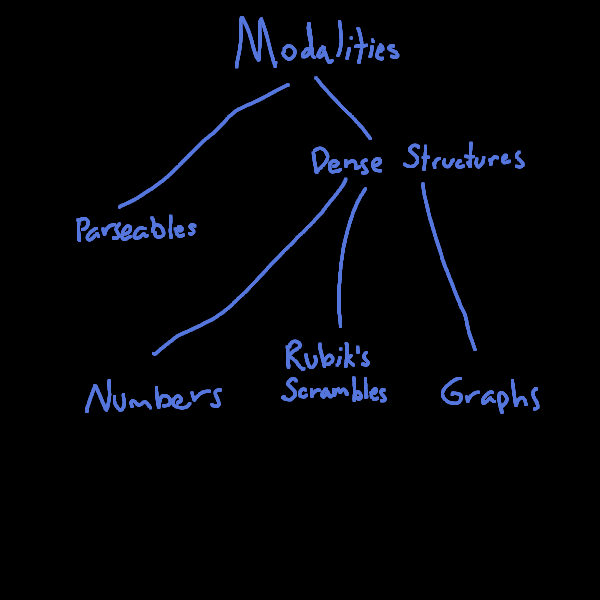
Another cluster could be labelled "Dense Mathematical Structures," containing numbers, graphs, rubiks cube scrambles (are all elements of a particular group.)