Friday Puzzle #1: Fundamentally Periodic
Periodic functions f(x) are functions for which you can "shift" by some positive value T on the x-axis such that the shifted function f'(x) lands on where f(x) was. That is to say, f(x+T) = f(x) for all x. We call T a "period" of f. Thus, 2pi is a period of the sine function. But... so are 4pi, 6pi, and so on! It should be clear that 2pi is the smallest period of sine - we will call the smallest period of a function its fundamental period.
Can you think of a real-valued function which is periodic, but does not have a fundamental period? A simple example is f(x)=c for any constant c. See if you can find one which isn't constant, or prove that there is no such function!
Extra credit: Can you find one such that the image of the reals under f is any arbitrary set of my choosing?
Can you think of a real-valued function which is periodic, but does not have a fundamental period? A simple example is f(x)=c for any constant c. See if you can find one which isn't constant, or prove that there is no such function!
Extra credit: Can you find one such that the image of the reals under f is any arbitrary set of my choosing?
Friday Puzzle #2: Four-Tour
A "knight's tour" is a path that a knight could take on a chessboard to touch every square exactly once. For this problem, we are concerned with closed knight's tours - the knight must end up back where it started.
Is it possible for a knight to make a closed tour on any chessboard of size 4xN? Find an example or prove that it is impossible!
Extra Credit: Find the set of all M, N such that a closed knight's tour on an MxN chessboard is possible.
Is it possible for a knight to make a closed tour on any chessboard of size 4xN? Find an example or prove that it is impossible!
Extra Credit: Find the set of all M, N such that a closed knight's tour on an MxN chessboard is possible.
Friday Puzzle #3: Cyclical Derivatives
We all know that differentiating f(x)=sin(x) 4 times, we get f''''(x)=sin(x). We thus call sin "4-cyclical." But, importantly, we do not call it 8-cyclical.
Formally, a function f(x) is n-cyclical, for some positive integer n, if the nth derivative of f with respect to x equals f, and there is no positive integer m<n such that the mth derivative of f equals f.
There are well-known examples of 1-cyclical, 2-cyclical, and other 4-cyclical functions. Can you name them? Can you name a function which has a different cycle, like 3 or 8? Or, more generally, can you find an indexed class of functions f_n(x) such that f_n is n-cyclic?
Formally, a function f(x) is n-cyclical, for some positive integer n, if the nth derivative of f with respect to x equals f, and there is no positive integer m<n such that the mth derivative of f equals f.
There are well-known examples of 1-cyclical, 2-cyclical, and other 4-cyclical functions. Can you name them? Can you name a function which has a different cycle, like 3 or 8? Or, more generally, can you find an indexed class of functions f_n(x) such that f_n is n-cyclic?
Friday Puzzle #4: Mosaic Theory
Attached in the picture are a few examples of "mosaics", along with their names.

A mosaic is a large rectangle, subdivided into a finite number of rectangles. The final example is not a mosaic because it contains a non-rectangular shape.
We call "a" the trivial mosaic.
We don't care about the specific representation of a mosaic, which is why the two mosaics labeled "d" are equal. However, two mosaics which are mirrored images, or differ rotationally by some multiple of 90 degrees, are not equal, hence b is not equal to c.
We can compose and decompose mosaics - for example, mosaic d can be constructed as a composition c(b), since b is placed into one rectangle of c. Note b(c) is not equal to d, and also note that c(b) is not uniquely d. Similarly to multiplication on the integers, if a nontrivial mosaic cannot be written as a composition of two nontrivial mosaics, we call it prime.
Now, for the questions:
1. How many prime mosaics are there?
2. Are there any prime mosaics which are not self-symmetric in terms of rotation or reflection?
3. Is the prime decomposition of a mosaic unique, just like the integers? What about if we disregard ordering of the composition, would it then be unique? What about if we disregard both ordering, and repetition?
4. (extra credit) If we permit infinitely many rectangles in a mosaic, is the set of primes then countably infinite or uncountably infinite? What if we then require a positive epsilon to be less than all constituent rectangles' areas?

A mosaic is a large rectangle, subdivided into a finite number of rectangles. The final example is not a mosaic because it contains a non-rectangular shape.
We call "a" the trivial mosaic.
We don't care about the specific representation of a mosaic, which is why the two mosaics labeled "d" are equal. However, two mosaics which are mirrored images, or differ rotationally by some multiple of 90 degrees, are not equal, hence b is not equal to c.
We can compose and decompose mosaics - for example, mosaic d can be constructed as a composition c(b), since b is placed into one rectangle of c. Note b(c) is not equal to d, and also note that c(b) is not uniquely d. Similarly to multiplication on the integers, if a nontrivial mosaic cannot be written as a composition of two nontrivial mosaics, we call it prime.
Now, for the questions:
1. How many prime mosaics are there?
2. Are there any prime mosaics which are not self-symmetric in terms of rotation or reflection?
3. Is the prime decomposition of a mosaic unique, just like the integers? What about if we disregard ordering of the composition, would it then be unique? What about if we disregard both ordering, and repetition?
4. (extra credit) If we permit infinitely many rectangles in a mosaic, is the set of primes then countably infinite or uncountably infinite? What if we then require a positive epsilon to be less than all constituent rectangles' areas?
Friday Puzzle #5: Board Games with Alice and Bob
1. Alice and Bob are playing a game. They take turns placing circular discs of equal radius inside of a larger disc whose radius is 5 times that of the small discs. Whomever is the first to be unable to fit a disc loses. Should Alice choose to go first or second? What would her strategy be?
2. Alice and Bob now play a game where they take turns placing coins in the squares of a 4x4 chessboard. Whomever is first to place a coin which is in the 8 bordering squares of an existing coin loses. Should Alice choose to go first or second? What would her strategy be? Arbitrary odd-sized boards? (extra credit: what about arbitrary even size? I don't know the answer.)
3. Alice and Bob are playing a game on pencil and paper. They each have a private piece of paper. Both begin by writing the digits 1-9 on the paper, in no particular configuration. They take turns calling out a number, above which both players write the initial of the player who called it. In writing ones initial over a number, that player "claims" that number. Once either player has a subset of size 3 of their claimed numbers which adds up to 15, that player wins. Alice immediately realizes a strategy which allows her to consistently tie with Bob without thinking too hard about what to do, regardless of whether she goes first or second. Can you find out Alice's secret strategy?
2. Alice and Bob now play a game where they take turns placing coins in the squares of a 4x4 chessboard. Whomever is first to place a coin which is in the 8 bordering squares of an existing coin loses. Should Alice choose to go first or second? What would her strategy be? Arbitrary odd-sized boards? (extra credit: what about arbitrary even size? I don't know the answer.)
3. Alice and Bob are playing a game on pencil and paper. They each have a private piece of paper. Both begin by writing the digits 1-9 on the paper, in no particular configuration. They take turns calling out a number, above which both players write the initial of the player who called it. In writing ones initial over a number, that player "claims" that number. Once either player has a subset of size 3 of their claimed numbers which adds up to 15, that player wins. Alice immediately realizes a strategy which allows her to consistently tie with Bob without thinking too hard about what to do, regardless of whether she goes first or second. Can you find out Alice's secret strategy?
Friday Puzzle #6: Mysterious Sequence
Find x in the following sequence:
1 11 21 1211 111221 312211 x ...
1. Compute y by repeatedly summing the digits of x until a one-digit number is reached.
2. Prove that the sequence never contains the digit y.
3. Can you find a different starting value for which the sequence has a different behavior, other than eventually exploding to infinity?
4. Prove that every element of the sequence contains the digit 1.
1 11 21 1211 111221 312211 x ...
1. Compute y by repeatedly summing the digits of x until a one-digit number is reached.
2. Prove that the sequence never contains the digit y.
3. Can you find a different starting value for which the sequence has a different behavior, other than eventually exploding to infinity?
4. Prove that every element of the sequence contains the digit 1.
Friday Puzzle #7: Kidnapped
1. Jeff Bezos, desperate for rocketry talent, kidnaps 100 SpaceXers and puts them in a large room to design him new rocket engines. To kidnap them, he used a special sleep potion which has the side effect of causing a green dot or red dot to appear on the back of each person's neck. If the green dot appears, the individual will be safe, but if a red dot appears, the person has a chance of dying at random if the antidote, which Bezos possesses, is not administered promptly. Bezos says that the SpaceXers can request to leave at any time, but of course the SpaceXers wouldn't dare leave without being certain they have a green dot. He removes all reflective surfaces from the room and prohibits communication so that no one can find out the color of their dot, but of course everyone can see everyone else's dot. After international outcry, Bezos permits one person (you!) to visit the SpaceXers, but he gives you strict rules of what you can tell them: you can only say one short sentence to the crowd, you can not command them to do anything, and any statement of fact that you make must be already known by everyone in the room. Upon arriving, you notice that no one has a red dot! What can you say to save the SpaceXers to save them as quickly as possible?
2. The 100 SpaceXers, now having escaped, are gathered at the entrance of a room. Inside, there are 100 boxes, each with a unique name written on top, belonging to one of the 100 people. Inside each box is the wallet of one of the SpaceXers, which contains their ID and money. However, the wallets have been shuffled randomly among the boxes such that the wallet's owner is not necessarily the name written on the top of the box. The SpaceXers will enter the second room one by one, and are permitted to open 50 boxes. If they locate their wallet within those 50 attempts, they will leave it where it is, but take note of the name on the box. That SpaceXer will then be quarantined without the option to communicate with the others, and the next SpaceXer will enter. Once complete, if all of the SpaceXers can correctly state the name on the box containing their wallet, they are all allowed to keep their money, but if one person fails then they all lose their money. The task is explained while they are together, and they are allowed to communicate until their turn entering the room. What should they do?
2. The 100 SpaceXers, now having escaped, are gathered at the entrance of a room. Inside, there are 100 boxes, each with a unique name written on top, belonging to one of the 100 people. Inside each box is the wallet of one of the SpaceXers, which contains their ID and money. However, the wallets have been shuffled randomly among the boxes such that the wallet's owner is not necessarily the name written on the top of the box. The SpaceXers will enter the second room one by one, and are permitted to open 50 boxes. If they locate their wallet within those 50 attempts, they will leave it where it is, but take note of the name on the box. That SpaceXer will then be quarantined without the option to communicate with the others, and the next SpaceXer will enter. Once complete, if all of the SpaceXers can correctly state the name on the box containing their wallet, they are all allowed to keep their money, but if one person fails then they all lose their money. The task is explained while they are together, and they are allowed to communicate until their turn entering the room. What should they do?
Friday Puzzle #8: Bonus Round
1. Prove that any prime p>3 has 24|p^2-1
2. Can you fill all the squares of an 8x8 chessboard EXCEPT 2 opposite corners using dominoes of size 1x2?
3. Can you fill all the squares of a 12x12 chessboard EXCEPT the middle 4 squares using T-tetrominoes?
2. Can you fill all the squares of an 8x8 chessboard EXCEPT 2 opposite corners using dominoes of size 1x2?
3. Can you fill all the squares of a 12x12 chessboard EXCEPT the middle 4 squares using T-tetrominoes?
Friday Puzzle #9: Pebbling a Chessboard
1. You have an 8x8 checkerboard with 3 pebbles on it. One is in the top left and the other two are in the adjacent 2 spots. You are allowed one type of move: you can remove any single pebble, in turn placing one in the spot below it and one in the spot to the right. However, you can only perform this move if the two spots which you place the pebbles in are already empty. That is to say, you can never have two pebbles in one square. Is there some sequence of moves which permits you to evacuate the three spaces which originally had pebbles? An example of a legal set of starting moves is shown below, where the moves were employed on the spaces with "."s
2. You now have a checkerboard with pebbles covering every space in the lower half of the board. This time, the pebbles move as follows: a pebble can jump over a single adjacent (not diagonal!) space with a pebble on it into the next empty space, in turn removing the pebble which was jumped over. Thus, a valid first move is of the following form:
How far up can a pebble reach? Can they get to the top row? Can they "jump out" of the top of the board? What about with an infinite board?
+---- +---- +---- +---- |oo |o.o |o.o |o.o |o |oo |o.o |o..o | | | o | oo
2. You now have a checkerboard with pebbles covering every space in the lower half of the board. This time, the pebbles move as follows: a pebble can jump over a single adjacent (not diagonal!) space with a pebble on it into the next empty space, in turn removing the pebble which was jumped over. Thus, a valid first move is of the following form:
+--------+ | | | | | | | o | |oooooo o| |oooooo o| |oooooooo| |oooooooo| +--------+
How far up can a pebble reach? Can they get to the top row? Can they "jump out" of the top of the board? What about with an infinite board?
Friday Puzzle #10: Hatted Logicians
1.
2.
3.
0 1 2 3 o- o- o- | -o ⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿These are 4 logicians, named 0, 1, 2, and 3, with their noses shown to depict the direction they are facing. They have been buried in the sand by a hysteric hat enthusiast named Jeff Bezos, and can't turn around. There is a wall separating the last one. They are told that there are 2 black and 2 white hats among them. However, they only know the colors of the hats which they can see. As soon as any single one of them shouts out their own hat color, they are all set free. If anyone says anything other than their correct hat color, Bezos will sue all of them (we don't want that!). Is it possible for them to always get set free, regardless of who is given what hat? What is their strategy?
2.
0 1 2 3 4 ... n o- o- o- o- o- ... o- ⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿Infuriated with the cleverness of the 4 logicians, Bezos decides to up the ante. He buries n logicians in a line, each one looking at the back of the person in front of them (such that they can see all hats in front of them.) Each one has a hat which is either red, green, or blue. They each must guess their hat color, and the group is freed if no more than one person says the wrong color. If anyone guesses anything other than a valid color, they are all sued. They're allowed to strategize ahead-of-time. What should the logicians do?
3.
0 1 2 3 4 ... -> o- o- o- o- o- ... -> ⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿⠿ ->Bezos repeats the previous exercise, with infinitely many logicians in the line, one for each non-negative integer such that n+1 is the nearest logician in front of n. This time, the group is freed if only finitely many people get their hat color wrong. What should they do?
Friday Puzzle #11: Off to the Races
1. A farmer has 25 horses and a race track which can fit 5 horses side-by-side. Each horse deterministically runs the track in some constant amount of time with no deviation. However, he does not have a stopwatch to time them, so he must choose to race them side by side. What is the fewest number of races required to identify the fastest, second fastest, and third fastest horses?
2. The farmer invests in a track which fits 25 horses side-by-side. He now makes the following claim: "I am thinking of a mapping of horses to tracks. With this mapping, every subset of exactly 6 horses has some horse which is left of a slower horse, and also has some horse which is right of a slower horse." Can you find such a mapping?
3. (Extra Credit) Find how many such mappings there are.
(Note: we assume that no two horses have equal speed.)
2. The farmer invests in a track which fits 25 horses side-by-side. He now makes the following claim: "I am thinking of a mapping of horses to tracks. With this mapping, every subset of exactly 6 horses has some horse which is left of a slower horse, and also has some horse which is right of a slower horse." Can you find such a mapping?
3. (Extra Credit) Find how many such mappings there are.
(Note: we assume that no two horses have equal speed.)
Friday Puzzle #12: Intuitive Summations
It is said that a young Gauss was asked by his grade school math teacher to sum the numbers from one to one hundred as an exercise in addition. Instead of going through the arithmetic effort, he noticed that he could add opposite numbers (1+100=101, 2+99=101, 3+98=101, ...) of which there were 50 pairs. He instantly responded 5050 (101*50,) astonishing the teacher. From this general strategy we can derive the well-known fact that 1+2+...+n = n(n+1)/2. We can reinforce this idea geometrically with the following diagram in the case of n=3, where each "L" shape represents the sum, and we combine two of them to make a rectangle with dimentions n * (n+1).
Today's puzzle is to extend this intuitive method of summation using geometry. The following summations can all be expressed in similar geometric fashion. Can you derive the formulas for them with this method? (First, try to derive the formula on your own, and if you get stumped, then peek at the formula and design your proof accordingly!)
In approximately increasing difficulty:
1. 1+3+5+7+...+n
2. 12 + 23 + 34 + ... + (n-1)n
3. 1^2 + 2^2 + 3^2 + ... + n^2
4. 1(n-1) + 2(n-2) + ... + (n-1)*1
5. (1) + (1+2) + (1+2+3) + ... + (1+2+...+n)
6. 1^3 + 2^3 + 3^3 + ... + n^3
+--------+ +--+ | | | | +-----+--+ +--+--+ | | | | +--+--+ +--+-----+ | | | | +--+ +--------+
Today's puzzle is to extend this intuitive method of summation using geometry. The following summations can all be expressed in similar geometric fashion. Can you derive the formulas for them with this method? (First, try to derive the formula on your own, and if you get stumped, then peek at the formula and design your proof accordingly!)
In approximately increasing difficulty:
1. 1+3+5+7+...+n
2. 12 + 23 + 34 + ... + (n-1)n
3. 1^2 + 2^2 + 3^2 + ... + n^2
4. 1(n-1) + 2(n-2) + ... + (n-1)*1
5. (1) + (1+2) + (1+2+3) + ... + (1+2+...+n)
6. 1^3 + 2^3 + 3^3 + ... + n^3
Friday Puzzle #13: Hex
Hex is among the board games with the simplest rulesets, while still having complex emergent behavior. It was studied by Conway, among other mathematicians, in the mid-1900s.
The rules are simple: two players, Red and Blue take turns coloring hexagons on the grid depicted. The first player to connect the opposite sides of their color with hexagons of their own color wins. That is, red wants to connect the two red sides with red hexagons, and blue wants to connect the two blue sides with blue hexagons.
The three challenges are below. In addition, prove there can't be a tie!
Blue to move:

Red to move:

Red to move:
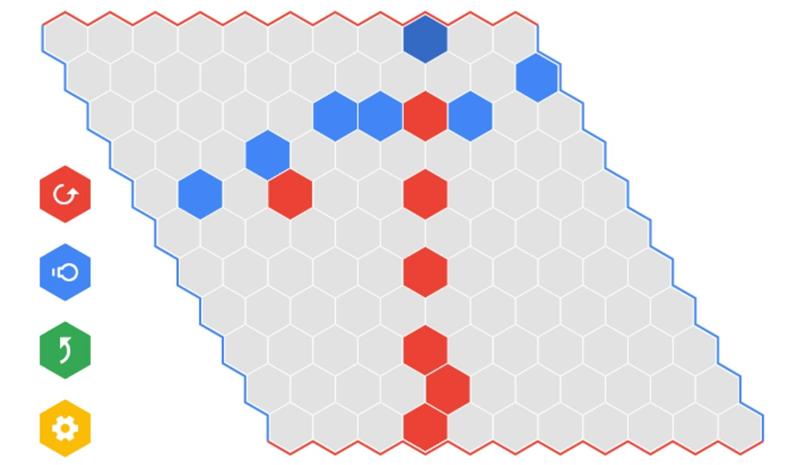
The rules are simple: two players, Red and Blue take turns coloring hexagons on the grid depicted. The first player to connect the opposite sides of their color with hexagons of their own color wins. That is, red wants to connect the two red sides with red hexagons, and blue wants to connect the two blue sides with blue hexagons.
The three challenges are below. In addition, prove there can't be a tie!
Blue to move:

Red to move:

Red to move:

Friday Puzzle #14: Rogue Computers
There are 100 computers, and each one is either 'good' or 'broken'. You can query any computer for the status of any other computer: a good computer will give you the correct answer, while a broken computer will give a random answer. For example, if you ask a good computer about a broken computer, it'll say 'broken', but if you ask a broken computer about a good computer, it may answer either 'good' or 'broken'. Broken computers, however, behave deterministically: they will always answer the same question in the same way.
1. Show that if you know that 50 or fewer of the computers are good, it is impossible to guarantee that you can find any good computer.
2. Show that if you know that more than 50 of the computers are good, you can determine the status of each computer.
3. Letting there be at least 51 good computers, come up with a strategy to efficiently identify one 'good' computer. Using your strategy, what is the fewest number of questions required to confidently identify one good computer (in the worst case?)
Puzzle credit to Grant Posner
1. Show that if you know that 50 or fewer of the computers are good, it is impossible to guarantee that you can find any good computer.
2. Show that if you know that more than 50 of the computers are good, you can determine the status of each computer.
3. Letting there be at least 51 good computers, come up with a strategy to efficiently identify one 'good' computer. Using your strategy, what is the fewest number of questions required to confidently identify one good computer (in the worst case?)
Puzzle credit to Grant Posner
Friday Puzzle #15: Hopscotch
+--+--+ | | | +--+--+--+--+ | | | | | +--+--+--+--+ | | | +--+--+The pattern above is drawn in chalk. Your job is to jump from square to square, but in each jump you may not jump to a square which is adjacent to your current square, or immediately diagonal to it. You can start on any square, and you must jump on each square exactly once. How do you do it?
(Extra Credit) prove that there is exactly one unique solution, along with its rotations and reflections.
Friday Puzzle #16: MU-puzzle
We are given the alphabet with the letters M, I, and U. We let "x" or "y" signify an arbitrary string of those letters. Then, we define functions a, b, c, d as follows:
In other words, can you derive MU when given only the beginning string MI, using the rules provided?
This riddle is from GEB:EGB by Douglas Hofstadter.
Formal rule Informal explanation Example a(xI) = xIU Add a U to the end of any string ending in I a(MI) = MIU b(Mx) = Mxx Double the string after the M b(MIU) = MIUIU c(xIIIy) = xUy Replace any III with a U c(MUIIIU) = MUUU d(xUUy) = xy Remove any UU d(MIUU) = MICan you find some composition "f" of the functions a, b, c, d such that f(MI) = MU?
In other words, can you derive MU when given only the beginning string MI, using the rules provided?
This riddle is from GEB:EGB by Douglas Hofstadter.
Friday Puzzle #17: Probabilities and Triangles and Circles
1. If you have a unit circle, and cut it at three randomly selected points, subsequently straightening out the 3 resultant arcs, what is the probability that they can form a triangle?
2. Choosing 3 points at random on the unit circle, this time the vertices of a triangle T, what is the probability the origin is inside of T?
2. Choosing 3 points at random on the unit circle, this time the vertices of a triangle T, what is the probability the origin is inside of T?
Friday Puzzle #18: Witch Coins, Which Coin?
You and a friend have been captured by a witch. She presents to you (but not your friend) a 64-square chessboard with a coin randomly flipped to either heads or tails on each square. She points out to you a particular coin on the chessboard -- the "target coin". You must then flip a single coin of your choosing.
Then, she takes the board and coins and hands it to your friend, who doesn't know the initial board state, the target coin, or which coin you flipped. Your friend must, just by looking at the current board state, determine which coin is the target coin to be freed.
Not all is lost, though -- the witch allows you and your friend to collaborate on a strategy ahead-of-time, but to reiterate, once she hands you the board and coins, the only communication is that you flip over a single coin of your choice.
What strategy do you use to flip the coin, and how does your friend determine the target square?
Puzzle courtesy of Grant Posner
Then, she takes the board and coins and hands it to your friend, who doesn't know the initial board state, the target coin, or which coin you flipped. Your friend must, just by looking at the current board state, determine which coin is the target coin to be freed.
Not all is lost, though -- the witch allows you and your friend to collaborate on a strategy ahead-of-time, but to reiterate, once she hands you the board and coins, the only communication is that you flip over a single coin of your choice.
What strategy do you use to flip the coin, and how does your friend determine the target square?
Puzzle courtesy of Grant Posner
Friday Puzzle #19: Twisty Puzzles
I am quite the fan of puzzles which resemble permutation groups with limited operations. Nobody solved the 15-puzzle question from Friday Puzzle #8, so here it is again, back with a vengeance! The questions are in increasing difficulty.
1. How many legal states are there on a 2x2x2 Rubik's Cube?
2. How many legal states are there on a normal (3x3x3) Rubik's Cube?
3. How many legal states are there on a 2x2x2 Rubik's Cube, when you are only permitted to twist faces 180 degrees?
4. How many legal states are there on a 15-puzzle?
To prove that an answer for such questions is correct typically involves proving that some lower bound on the number of legal states equals some upper bound. This Friday, your task is to correctly identify the number of legal states, and prove that it is an upper bound. For extra credit, prove it is also a lower bound, which tends to be a lot harder!
The 15 puzzle (attached) involves sliding tiles such that the numbers count from 0 to 15 as pictured.
(Bonus: can you prove that the group involved in question 3 is isomorphic to some other well-known group?)
1. How many legal states are there on a 2x2x2 Rubik's Cube?
2. How many legal states are there on a normal (3x3x3) Rubik's Cube?
3. How many legal states are there on a 2x2x2 Rubik's Cube, when you are only permitted to twist faces 180 degrees?
4. How many legal states are there on a 15-puzzle?
To prove that an answer for such questions is correct typically involves proving that some lower bound on the number of legal states equals some upper bound. This Friday, your task is to correctly identify the number of legal states, and prove that it is an upper bound. For extra credit, prove it is also a lower bound, which tends to be a lot harder!
The 15 puzzle (attached) involves sliding tiles such that the numbers count from 0 to 15 as pictured.
(Bonus: can you prove that the group involved in question 3 is isomorphic to some other well-known group?)
Friday Puzzle #20: Dot-Boxes
We consider a chessboard which is n squares wide and n squares tall.
We then wish to place n dots in the centers of the squares, with a certain condition: every length between dots is unique.
In the 2x2 case, this is trivial:
Here is an example of an INCORRECT solution for n=3:
Can you find a solution to the n=3 case? What about n=4 and higher? I'll let this be something of a competition to see who can come up with the biggest solution.
Extra credit: Prove that there is some m, such that for all n>m, no board of size n has a solution.
We then wish to place n dots in the centers of the squares, with a certain condition: every length between dots is unique.
In the 2x2 case, this is trivial:
+---+---+ | * | * | +---+---+ | | | +---+---+There is only one distance here, length 1, so of course it is unique.
Here is an example of an INCORRECT solution for n=3:
+---+---+---+ | * | | | +---+---+---+ | | * | | +---+---+---+ | * | | | +---+---+---+We see that one connection is length 2, and 2 connections are length sqrt(2). Since we have 2 lengths which are equal, this is not a solution.
Can you find a solution to the n=3 case? What about n=4 and higher? I'll let this be something of a competition to see who can come up with the biggest solution.
Extra credit: Prove that there is some m, such that for all n>m, no board of size n has a solution.
Friday Puzzle #21: Close Contact
Find 4 circles such that every pair is tangent (touch at exactly one point.)
Find 6 spheres such that every pair is tangent (touch at exactly one point.)
Recall that a circle, or sphere, is defined as the set of points which are all some positive distance d from the center.
Note: You may not extend the dimension of the problem- for problem 1, you must solve it in 2-space and problem 2 must be solved in 3-space.
Find 6 spheres such that every pair is tangent (touch at exactly one point.)
Recall that a circle, or sphere, is defined as the set of points which are all some positive distance d from the center.
Note: You may not extend the dimension of the problem- for problem 1, you must solve it in 2-space and problem 2 must be solved in 3-space.
Friday Puzzle #22: Equilateral Bowling
A mathematically inclined bowler considers the standard 10-pin configuration:
1. What is the fewest number of pins which can be removed such that there remains no equilateral triangle with vertices defined by the the centers of 3 pins?
2. Can the bowler paint some amount of the white pins black such that there is no equilateral triangle have vertices entirely by white pins or entirely by black pins?
o o o o o o o o o oand arrives at the following questions:
1. What is the fewest number of pins which can be removed such that there remains no equilateral triangle with vertices defined by the the centers of 3 pins?
2. Can the bowler paint some amount of the white pins black such that there is no equilateral triangle have vertices entirely by white pins or entirely by black pins?
Friday Puzzle #23: Number of Numbers
Your task will be to fill out row 2 with single digit integers (0-9):
For example, the following solution is incorrect: it says there are no digits 1-9 which is true, but also claims that there are no 0 entries on row 2, of which there are clearly actually ten.
Problem 2: Find the set of ALL solutions (and prove your result.)
Problem 3: Instead of considering the base-10 problem only, find the set of ALL solutions for some arbitrary base n.
Row 1: 0123456789 Row 2: ??????????The rule: If some digit "d" is written below a number "n" in row 1, that means "n" must appear "d" times in row 2.
For example, the following solution is incorrect: it says there are no digits 1-9 which is true, but also claims that there are no 0 entries on row 2, of which there are clearly actually ten.
0123456789 0000000000Problem 1: Solve row 2 as the problem is stated
Problem 2: Find the set of ALL solutions (and prove your result.)
Problem 3: Instead of considering the base-10 problem only, find the set of ALL solutions for some arbitrary base n.
Friday Puzzle #24: Polite Graph Theorists
A group of graph theorists meet at a conference, and some pairs of them shake hands.
1. Show that the amount of graph theorists who shook hands an odd number of times is even.
2. Given that there are 6 graph theorists present, demonstrate that there is either a subgroup of 3 graph theorists who all shook hands with each other, or a subgroup of 3 among whom no hands were shook.
1. Show that the amount of graph theorists who shook hands an odd number of times is even.
2. Given that there are 6 graph theorists present, demonstrate that there is either a subgroup of 3 graph theorists who all shook hands with each other, or a subgroup of 3 among whom no hands were shook.
Friday Puzzle #25: Knot so fast!
1. Can you do the following?
-Lay a rope (Or phone charger, or whatever) flat in a straight line on a table.
-Simultaneously pick up one end in each hand.
-Without letting go, tie an overhand knot (the most simple kind of knot.) https://en.wikipedia.org/wiki/Overhand_knot
-Place the rope back down on the table, simultaneously letting go of both ends at the same time.
2. You wish to hang a picture on the wall by attaching a string to the top of it, and then placing 2 pins in the wall to hold it up. The puzzle: You must find a way to arrange the rope around the 2 pins such that if either individual pin is removed, the painting falls down, but with both pins present the painting is held in place.
3. Do the same thing, but with 3 pins, such that upon removal of any, it drops.
4. Find a meaningful connection between problem 2 and the idea of a commutator in group theory.
-Lay a rope (Or phone charger, or whatever) flat in a straight line on a table.
-Simultaneously pick up one end in each hand.
-Without letting go, tie an overhand knot (the most simple kind of knot.) https://en.wikipedia.org/wiki/Overhand_knot
-Place the rope back down on the table, simultaneously letting go of both ends at the same time.
2. You wish to hang a picture on the wall by attaching a string to the top of it, and then placing 2 pins in the wall to hold it up. The puzzle: You must find a way to arrange the rope around the 2 pins such that if either individual pin is removed, the painting falls down, but with both pins present the painting is held in place.
3. Do the same thing, but with 3 pins, such that upon removal of any, it drops.
4. Find a meaningful connection between problem 2 and the idea of a commutator in group theory.
Friday Puzzle #26: Amorous Aphids
4 bugs, at the corners of a 1km-wide square, are arranged as follows, with arrows indicating the direction they are facing:
No calculus is necessary.
> v ^ <They walk at a constant rate of 1km/h, but continuously turn to keep facing the bug they were originally looking at. Eventually, they will all make contact. How long is the path each bug will walk before making contact?
No calculus is necessary.
Friday Puzzle #27: Wooden Cubes
A carpenter has a 3 inch by 3 inch cube, and a saw that can make planar cuts through the cube. It is clear that he can cut the cube into 27 1-inch cubies with 6 cuts, but if he rearranges the blocks between cuts, is it possible that he can do it in fewer than 6 cuts?
Unfortunately for the carpenter, a termite gets to the cube first! It burrows its way into a cubie which has external surface, and then works its way eating a path through the cube, passing through all cubies exactly once, always burrowing from cubie to adjacent cubie (no diagonal moves.) Is there a path it can take such that it finishes in the center cubie?
A desk calendar has 2 cubes on it, where each face of a cube features a digit, so that the cubes can be oriented in a way to write any date from 01 to 31. Determine the layout of the cubes!
Unfortunately for the carpenter, a termite gets to the cube first! It burrows its way into a cubie which has external surface, and then works its way eating a path through the cube, passing through all cubies exactly once, always burrowing from cubie to adjacent cubie (no diagonal moves.) Is there a path it can take such that it finishes in the center cubie?
A desk calendar has 2 cubes on it, where each face of a cube features a digit, so that the cubes can be oriented in a way to write any date from 01 to 31. Determine the layout of the cubes!
Friday Puzzle #28: Arrow Game
This is a single-player board game. An example start position is as such:
1. move one spot
2. jump over a single arrow
Here are two sample first moves
It also automatically solves them too (with -r flag)... but don't cheat please!
>>>> <<<<Arrows can make 2 types of move, only moving in the direction it points into an open spot.
1. move one spot
2. jump over a single arrow
Here are two sample first moves
>>>> <<<< (starting position) >>> ><<<< (move type 1) >>><> <<< (move type 2)We say that a board has been solved when every arrow can only "see" (directly in its line of sight) arrows of its same type, and walls (denoted #.) Thus, the board provided has this unique solution:
<<<< >>>>Today's challenge: Mark all of the following boards as solvable or unsolvable. If unsolvable, prove it. Problems are listed in increasing difficulty.
1. >>>> <<<< 2. >vv > < ^^< 3. >vvvv > <<< ^^<<< ^^<<< ^^<<< 4. #>vv# >>vvv >> << ^^^<< #^^<# 5. >v>v>v ^<^<^< >v>v>v ^<^<^< >v>v>v ^<^<^ 6. >>vvv >>>vv >^ v< ^^<<< ^^^<< 7. ##vv## ##vv## >>>v<< >>^ << ##^^## ##^^## 8. >>vvv >>vvv >> << ^^^<< ^^^<< 9. >>>vvvv >>>vvvv >>>vvvv >>> <<< ^^^^<<< ^^^^<<< ^^^^<<<Although you can of course do them by hand, attached is a C++ program I threw together over the weekend which lets you attempt the puzzles. Use: compiled_program -h gridfile.arr and then type W/A/S/D and press enter to move.
It also automatically solves them too (with -r flag)... but don't cheat please!
Friday Puzzle #29: Minesweeper
I have a friend who is ranked #32 globally in Minesweeper. Sometimes she sends me puzzles like the following.
Determine what should be done next in the following boards.
1. (Easiest)

2.

3.
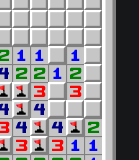
4. (Hardest)

1. (Easiest)

2.

3.

4. (Hardest)

Friday Puzzle #30: Weighted Coins
1. You have 9 coins, one of which weights slightly more than the others, along with a simple 2-sided scale which tells you which side is heavier. What is the fewest number of weighings required to identify the heavy coin?
2. You now have 13 coins, one of which is either lighter or heavier (you don't know which.) Now how many weighings are required?
2. You now have 13 coins, one of which is either lighter or heavier (you don't know which.) Now how many weighings are required?
Friday Puzzle #31: Irrational Rational Functions
Is there an increasing bijection from the rationals to the nonzero rationals?
Friday Puzzle #32: Quad-Quack-Quo
We wish to fill in a square grid with X's and O's such that there are no 4 letters of the same type which form the corners of a square.
For the sake of this problem, we will only consider "horizontally aligned" squares, meaning that the following solution is permissible despite a rotated square of 4 o's:
2. If we instead play this as an adversarial board game where players take turns (starting with x) placing their letter with the intent of constructing a square, is there any board size such that the second player would win (assuming perfect play?) Prove your result.
3. (Extra Credit) Explicitly find the function f, such that f(n) gives the winner {x, o, tie} on an n*n board assuming perfect play.
x o o o o x x x oThe above solution for a grid of size 3 is valid. However, the one below is not:
x o x o x x x x xIt is not valid because it has 2 squares defined by x's: the large square defined by the 4 corners, and the small square in the bottom right.
For the sake of this problem, we will only consider "horizontally aligned" squares, meaning that the following solution is permissible despite a rotated square of 4 o's:
x o x o x o o o x1. Either find the largest permissible grid, or demonstrate that there are arbitrarily large permissible grids.
2. If we instead play this as an adversarial board game where players take turns (starting with x) placing their letter with the intent of constructing a square, is there any board size such that the second player would win (assuming perfect play?) Prove your result.
3. (Extra Credit) Explicitly find the function f, such that f(n) gives the winner {x, o, tie} on an n*n board assuming perfect play.
Friday Puzzle #33: Covered Cubes
You have an infinite supply of 1cm^3 white cubes, and one black cube. What is the greatest number of white cubes which you can get to contact the black cube with positive area? Try the problem where the black cube has edge length of:
1. .001cm
2. 1cm
For extra credit, solve #2 but instead using tetrahedrons or other platonic solids!
1. .001cm
2. 1cm
For extra credit, solve #2 but instead using tetrahedrons or other platonic solids!
Friday Puzzle #34: A Cute Square
Segment a square into only acute triangles! Bonus points go to the solution with the fewest triangles.
Friday Puzzle #35: Burning Ropes
You are presented with a lighter along with 2 ropes soaked in oil. Each rope is known to take 1 hour to burn fom one end to the other, but they do not burn at a constant rate: you do not know how much of the rope will burn after, say, 30 minutes.
How do you use these tools to accurately measure 45 minutes?
How do you use a single rope to measure 15 minutes? An infinite number of actions is permitted.
(extra credit) What is the set of times that can be computed with a single rope? What about N ropes?
How do you use these tools to accurately measure 45 minutes?
How do you use a single rope to measure 15 minutes? An infinite number of actions is permitted.
(extra credit) What is the set of times that can be computed with a single rope? What about N ropes?
Friday Puzzle #36: Around the World
As the private owner of an infinitely large fleet of jets along with their pilots, you decide to fly all the way around the world. Your top-of-the-line jets are capable of transferring fuel among themselves mid-flight. However, there are some drawbacks: a full tank of fuel only takes you halfway around Earth's circumference. Furthermore you do not have permission to land, take off, or refuel from the ground anywhere other than your private runway, Crash-landing or running out of fuel mid-flight are not options (for you or your hired pilots.)
1. Find a strategy that permits you to make a full tour around the circumference of the earth.
2. Prove that your strategy minimizes fuel usage.
3. You decide to migrate all your jets to Flatland, a flat planet which extends infinitely in all directions, and establish a new runway there. What is the furthest distance you can reach by jet, and return safely?
1. Find a strategy that permits you to make a full tour around the circumference of the earth.
2. Prove that your strategy minimizes fuel usage.
3. You decide to migrate all your jets to Flatland, a flat planet which extends infinitely in all directions, and establish a new runway there. What is the furthest distance you can reach by jet, and return safely?
Friday Puzzle #37: Hydration Station
Some amount of cities (represented as points) are collectively trying to construct a single water tower to serve all of them. The underground tubing required is extremely expensive - they wish to minimize the total amount of tubing while maintaining redundancy such that when any tube breaks, at most one city is affected.
For example, in the case of 2 cities, the optimal position of the water tower is anywhere on the line segment connecting the cities.
Find simple strategies to determine the optimal placement of the water tower in the case of 3 and 4 cities. The strategies should be sufficiently simple that they can be validated with nothing but a compass and straight edge.
(Extra credit) Come up with a mechanical model for the problem which can determine the optimal solution for any amount of cities.
For example, in the case of 2 cities, the optimal position of the water tower is anywhere on the line segment connecting the cities.
Find simple strategies to determine the optimal placement of the water tower in the case of 3 and 4 cities. The strategies should be sufficiently simple that they can be validated with nothing but a compass and straight edge.
(Extra credit) Come up with a mechanical model for the problem which can determine the optimal solution for any amount of cities.
Friday Puzzle #38: Tom and Jerry
Jerry the mouse was relaxing in the center of a circular lake when he noticed that Tom the Cat was waiting at the perimeter to catch him. Tom runs at 4km/h on land (but cannot swim,) but Jerry can run infinitely fast, and swim at 1km/h.
1. Can Jerry escape the lake safely?
2. How fast is the fastest cat that Jerry could escape from?
1. Can Jerry escape the lake safely?
2. How fast is the fastest cat that Jerry could escape from?
Friday Puzzle #39: Torus Sudoku
+---+---+---+---+---+ | 1 | 2 | 3 | 4 | 5 | +---+---+---+---+---+ | | | | | X | +---+---+---+---+---+ | | | | X | | +---+---+---+---+---+ | | | 1 | | | +---+---+---+---+---+ | | X | | | | +---+---+---+---+---+
On a 5x5 grid, you wish to fill in all spots with the numbers 1-5 such that any 5 squares in a line must contain exactly one of each number. Lines may be either vertical, horizontal, or diagonal. Here's the catch: lines are allowed to "wrap" around the edge. How many valid solutions contain the top row "12345" as shown?
An example of an illegal entry is also shown on the diagram: the 1 placed on the 4th row is not allowed, since that 1, the 1 on the first row, and the 3 X's are all in a line of 5, meaning this line contains multiple 1s which is not allowed.
(Easy) Find a solution.
(Meduim) Find all solutions.
(Hard) Prove that there are no solutions which you did not provide in (2).
Friday Puzzle #40: Full Flow
In the popular phone game "flow," the user is presented with a grid, some of whose squares contain colored dots. The user is tasked with connecting the dots of the same color such that no pipes overlap.
Can you find an 8x8 flow puzzle setup with as few different colors as you can, such that the player is forced to fill the entire grid with piping? Below is an example solution using 11 colors, but you can do it with fewer!
A B C D E J K H . . . . . . K . . . . . . . J H . . . . . G . I . . . . . F . . . . . . . . . . . . . . . . . . A B C D E F G I
Friday Puzzle #41: Squares Mod 5
Show that no square can be written as 5n±2 for integer n.
Friday Puzzle #42: Swingset
Come up with a method to swing (generate an arbitrary amount of rotational momentum) on a swingset whose chains cannot be bent, without contacting either the ground or the rod from which the swing is suspended.
Friday Puzzle #43: Exponential Sample
Choose a very large number n, and then choose some x randomly in 0<x<n. What is the probability that e^x starts with the digit 1?
Friday Puzzle #44: Fast Primes
Suppose that you have a computer capable of performing any basic arithmetic operation (+, -, *, /) in exactly 1 millisecond, regardless of the size of the numbers.
What strategy could you use to quickly determine the exact number of primes between 1 and some very large n?
What strategy could you use to quickly determine the exact number of primes between 1 and some very large n?
Friday Puzzle #45: Metric Ants
1. There are 1,000 ants on a meter stick, walking either left or right. they all move at 1cm/s. If they get to the edge, they fall off. If they run into each other, the 2 colliding ants turn around and go the other way. Up to the initial positions of the ants, what is the longest time that could elapse between the start and when the last ant falls off?
2. Now, one ant is at the end of a stretchy meter stick, and begins to walk towards the other end. What constant speed must you stretch the meter stick such that the ant never reaches the end?
2. Now, one ant is at the end of a stretchy meter stick, and begins to walk towards the other end. What constant speed must you stretch the meter stick such that the ant never reaches the end?
Friday Puzzle #46: Parenthetically
We call a parenthetical expression "reducible" if there is an opening parenthesis followed by a closed parenthesis of the same type. Thus, ()[}{] reduces to [}{].
Consider ([)]. It is not reducible, but if we delete all parentheses of any type, either () or [], then the remainder of the expression reduces to nothing. The same holds for ([[)]] and ([)[(]]).
Those expressions only use 2 parenthesis types. Can you come up with one using 3? or n?
Hint: This problem is the exact same as a previous friday puzzle, from a different perspective. Can you find which?
Consider ([)]. It is not reducible, but if we delete all parentheses of any type, either () or [], then the remainder of the expression reduces to nothing. The same holds for ([[)]] and ([)[(]]).
Those expressions only use 2 parenthesis types. Can you come up with one using 3? or n?
Hint: This problem is the exact same as a previous friday puzzle, from a different perspective. Can you find which?
Friday Puzzle #47: Keen Queens
What is the fewest number of queens that you can put on a chessboard such that they collectively either occupy or attack all squares?
Friday Puzzle #48: Oriented Tilings
(Easy) Suppose you are walking on an infinite tightrope which is split into small sections of 1 meter, each section painted either black or white. You only ever want to walk in one direction and not the other, and thus you wish for the tightrope to be painted with some periodic pattern such that you can always tell which way is forward and which way is backward. What is the shortest such repeated oriented sequence? For example, coloring the sections B-W-W-B-W-W-B-W-W (repeated) would not work since looking backwards it would be the same pattern, just offset by one color (W-W-B-W-W-B-W-W-B...)
(Medium) Now suppose you are on an infinite grid, and the "pattern" is an infinitely tiled NxN super-square composed of 1x1 subsquares. You need to be able to always determine which direction is north, east, south, and west. What is the smallest N such that this can be accomplished?
(Hard) Try problem 2 again, but with this quirk: after you have painted the grid, some adversarial actor will arrive just to paint red over all squares except a single infinite "strip" of 1-meter width, either in the east-west direction or the north-south direction. You must then identify the cardinal directions. How can you initially paint the grid to guarantee you can still orient yourself?
(Medium) Now suppose you are on an infinite grid, and the "pattern" is an infinitely tiled NxN super-square composed of 1x1 subsquares. You need to be able to always determine which direction is north, east, south, and west. What is the smallest N such that this can be accomplished?
(Hard) Try problem 2 again, but with this quirk: after you have painted the grid, some adversarial actor will arrive just to paint red over all squares except a single infinite "strip" of 1-meter width, either in the east-west direction or the north-south direction. You must then identify the cardinal directions. How can you initially paint the grid to guarantee you can still orient yourself?
Friday Puzzle #49: Prime-Sum
Recently, the square-sum problem was solved! It asks, given the integers 1 to n, can you shuffle them around such that any 2 consecutive numbers add up to a square? It was proven that there is some m, such that all n>m have such sequences. Today's puzzle is to find all n such that, given the integers 1 to n, you can shuffle them around with consecutive pairs summing to a PRIME.
Thanks to Mitchell Haugen for telling me about the original problem!
Thanks to Mitchell Haugen for telling me about the original problem!
Friday Puzzle #50: Broken Bridge
Alice, Bob, Charlie, and Daniel arrive at a bridge in the dark, with one flashlight. The flashlight is required by any group crossing the bridge, and the bridge is only sturdy enough to hold two people at a time. They each take 1,2,5,10 minutes respectively to cross the bridge. What is the minimum time by which everyone can have crossed the bridge? Try to generalize the problem. What if the people walk at A≤B≤C≤D speeds? What about S₀≤S₁≤...≤Sₙ?
Friday Puzzle #51: Covering Sets
Consider a 2-dimensional plane, where each point starts off colored white. Our goal today will be coloring certain points black to avoid certain shapes with only one color. For the following scenarios, either provide a set of black points, or prove it impossible.
*Note, when I say 0% of the points being black, I mean this with respect to every epsilon-neighborhood given a uniform sample over area.
- Cover the plane with black points such that there is no entirely white line segment of length 1, and 0% of the plane is black.
- Cover the plane with black points such that there is no entirely white line segment of length 1, such that the set of black points is countable.
- Cover the plane with black points such that a line segment of ANY length contains both colors.
- Cover the plane with black points such that a filled circle of ANY radius contains both colors, only using countably many black points.
- (Extra Credit) Cover the plane with an uncountable amount of colors such that a line segment of ANY length contains all colors.
*Note, when I say 0% of the points being black, I mean this with respect to every epsilon-neighborhood given a uniform sample over area.
Friday Puzzle #52: Maximal Division
From the first 100 natural numbers, what is the largest subset of numbers that you can choose such that none divides any other?
Friday Puzzle #53: Tricky Triangle
Consider the following arrangement of 15 x's:
Can you find a solution? How many solutions are there? How many are geometrically distinct?
/ x \
/ x x \
/ x x x \
/ x x x x \
/ x x x x x \
-----------
Your job is to place the numbers 1 through 5 on the x's such that no line which is parallel to any of the 3 borders (denoted /, , -) touches 2 of the same number.
Can you find a solution? How many solutions are there? How many are geometrically distinct?
Friday Puzzle #54: Infinite Connect 4
Consider a rather strange variant of the game connect 4. In this variant, instead of working adversarially with your opponent, you are working collaboratively to achieve the result of a tie. Furthermore, the grid extends infinitely in every direction. If the board has equally many pieces of each color, it is easy to achieve a result of a tie. However, if there are more yellow pieces than red pieces, then it gets a bit tougher. The question: What is the smallest ratio of red pieces to yellow pieces such that a draw on the infinite board can be made?
A note for the nitpickers: since you can always biject the amount of red and yellow stones, the idea of a "ratio" here in the traditional sense doesn't really work. To formalize, we will define r(x,y,e) over a board as follows: r(x,y,e) is equal to the percentage of red stones to yellow stones partially contained in an epsilon neighborhood with radius e centered about point (x,y). We then define the red point ratio of the whole board as so: ratio_xy = lim r(x,y,e) as e approaches +inf overall_ratio = min(ratio_xy) over all (x,y)
A note for the nitpickers: since you can always biject the amount of red and yellow stones, the idea of a "ratio" here in the traditional sense doesn't really work. To formalize, we will define r(x,y,e) over a board as follows: r(x,y,e) is equal to the percentage of red stones to yellow stones partially contained in an epsilon neighborhood with radius e centered about point (x,y). We then define the red point ratio of the whole board as so: ratio_xy = lim r(x,y,e) as e approaches +inf overall_ratio = min(ratio_xy) over all (x,y)
Friday Puzzle #55: Odd Orbits
It's a well-known fact that the orbit of a small object around a larger one follows a conic section. Circular and elliptical orbits, along with parabolic and hyperbolic trajectories, are the only paths that such an object can follow. This is determined by the fact that the force of gravity degrades with a relationship of 1/r^2 to the distance between the objects. What if we permit different profiles of the force of gravity? If Fg=Gm1m2r instead of Fg=Gm1m2/r^2, then what orbital trajectories would be permitted in that universe? What about in general: If Fg=Gm1m2r^n for any real n?
Problem credit to Victor Hakim
Problem credit to Victor Hakim